Selles postituses tutvustan ühte kõige olulisemat statistilist (andmeteaduse) mudelit – regressiooni. See on mudel, mida enamik statistika- ja andmeteaduseraamatuid esimesena tutvustavad. Seda on lihtne arvutada, lihtne aru saada ja sellest saab keerulisemate mudelite juurde edasi minna.
Regressioone on mitut liiki, kuid täna peatun kõige klassikalisemal – lineaarsel regressioonil. See mudel eeldab, et kui kirjeldav tunnus muutub ühe ühiku võrra, siis uuritav tunnus muutub ühe konstandi jagu.
Need, kes on regressiooniga juba tuttavad, (või need, keda lihtsalt ei huvita,) võivad esimesed osad vahele jätta ja kohe kokkuvõtte juurde minna.
Teooria
See teooria osa põhineb Ene Kääriku Andmeanalüüs II loengukonspektil. See on üks mu lemmikuid konspekte ülikoolist.
Alustame ühe argumendiga lineaarse regressioonimudeliga ehk lihtsa lineaarse regressioonimudeliga, mille kuju on
Y = α +βX + ε,
kus Y on uuritav tunnus, X on kirjeldav tunnus, α on vabaliige, β on regressioonikordaja ja ε mudeli juhuslik viga (mille eeldustest võib lähemalt lugeda konspektist).

Mudeli parameetrid hinnatakse vähimruutude meetodil:
erinevused tegelikult mõõdetud uuritava tunnuse väärtuste ja mudeli järgi prognoositud väärtuste vahel minimiseeritakse.
Joonisel on sinisega märgitud regressioonisirge, punased on andmepunktid ning rohelised jooned tähistavad väärtusi, mille ruutusid minimeeritakse vähimruutude meetodiga. Eesmärgiks on leida selline sinine joon, mille korral roheliste joonte ruutude summa oleks kõige väiksem.
Kui tundub, et seda uuritavat tunnust mõjutavad rohkem kui ainult üks seletav tunnus, siis võib mudelisse lisada ka teisi kirjeldavaid tunnuseid X1, X2, X3 … , mille korral on mudeli kujuks
Y = α + β1X1 + β2X2 + β3X3 + … + ε,
kus Y on uuritav tunnus, X1, X2, X3 … on kirjeldavad tunnused, α on vabaliige, β1, β2, β3 … on regressioonikordajad ja ε mudeli juhuslik viga.
Mudelis peaks olema ainult sellised seletavad tunnused, mis on olulised (R’i mudel näitab iga tunnuse olulisust).
Mudeli headuse näitajaks loetakse determinatsioonikordajat R2. Determinatsioonikordaja näitab, kui suure osa uuritava tunnuse Y hajuvusest kirjeldab lineaarne regressioonimudel ehk mitu protsenti uuritavast tunnusest kirjeldab mudel. Mida suurem R2 seda parem mudel. Meie vaatame parandatud R2, mis teeb ülesobitamise keerulisemaks.
Lineaarse regressiooni kohta võib lisaks lugeda konspektist (peatükk 4) või Wikipediast.
PS! Siin postituses ma vigade eeldusi ei kontrolli.
Andmed
Mudeli tegemiseks on vaja andmeid. Selles postituses kasutan Eurostati andmeid 2014. aasta käsimüügiravimite kohta* ja Euroopa pealinnade ilmainfot**. Sellise seose peale tuli mu kolleeg Andres, kes nägi Eurostati raportis järgmist joonist.
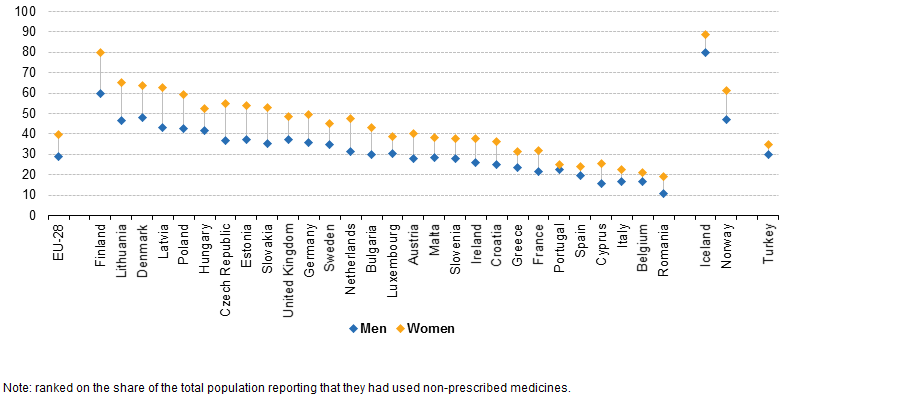
Ta tähendas, et põhjamaid tundub eesotsas rohkem, seega siin võiks olla seos ilmaga. Põhjas on külmem ja selle tõttu kasutatakse ka rohkem käsimüügiravimeid (nt nohu- ja köharohud, valuvaigistid).
Ehk uuritavaks tunnuseks on protsent inimestest, kes on viimase kahe nädala jooksul kasutanud käsimüügiravimeid (2014. aasta andmed). Kirjeldavad tunnused on ilma andmed.
Riigi keskmist ilma on raske hinnata, seega ma kasutan riigi pealinna ilma andmeid. Kui infot mõne riigi pealinna kohta ei leidnud, siis jätsin andmestikust välja.
Andmestikus on 29 riiki (Türgi ja Küpros jäid välja) ja 7 tunnust:
- riigi nimi,
- käsimüügiravimite kasutamise protsent,
- kuiste kõrgete temperatuuride maksimaalne vahe (tavaliselt juuli temp – veebruari temp) °C,
- aasta keskmine (kõrge) temperatuur °C,
- sademete hulk mm,
- sademetega päevade arv,
- päiksepaiste tundide arv.
R’i näide ja tulemused
Alustuseks loeme sisse vajalikud andmed ja paketid. Ja uurime andmeid lähemalt.
library(dplyr)
library(ggplot2)
andmed <- read.csv("ilm_ravim.csv")Ühe seletava tunnusega mudel
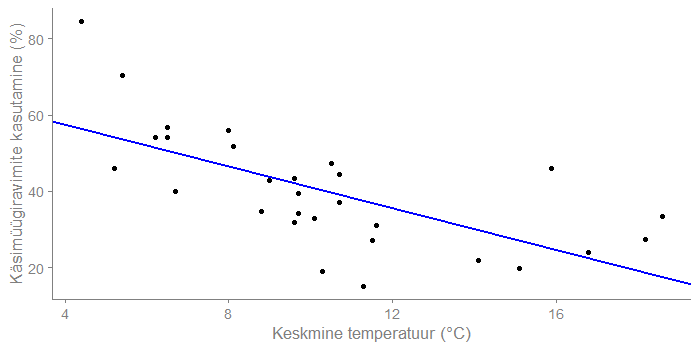
Enne mudeldamist tuleb andmetega tutvuda ja valida mudeliks vajalikud tunnused. Mina alustan mudeldamist keskmise temperatuuriga.
mudel1 <- lm(kasutusprotsent ~ kesk_temp, andmed)
summary(mudel1)
> Call:
> lm(formula = kasutusprotsent ~ kesk_temp, data = andmed)
>
> Residuals:
> Min 1Q Median 3Q Max
> -22.3006 -7.9678 -0.8705 6.2145 28.0899
>
> Coefficients:
> Estimate Std. Error t value Pr(>|t|)
> (Intercept) 68.3045 6.4471 10.595 4.05e-11 ***
> kesk_temp -2.7260 0.5881 -4.635 8.12e-05 ***
> ---
> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> Residual standard error: 11.85 on 27 degrees of freedom
> Multiple R-squared: 0.4431, Adjusted R-squared: 0.4225
> F-statistic: 21.48 on 1 and 27 DF, p-value: 8.121e-05
Mudeldamiseks kasutan Ri sisseehitatud funktsiooni lm(), mis soovib valemit Y ~ X1 + X2 + X3 + ... ja andmetabelit, kust neid tunnuseid otsida. summary() funktsioon näitab mudeli kuju. Tabeli viimane veerg näitab, millised tunnused on mudelis statistiliselt olulised (tõenäosus peab olema alla 0.05). Kui tunnus on oluline, siis on rea lõpus *, ** või ***. Selle mudeli R2 on 44% ja parandatud R2 on 42%.
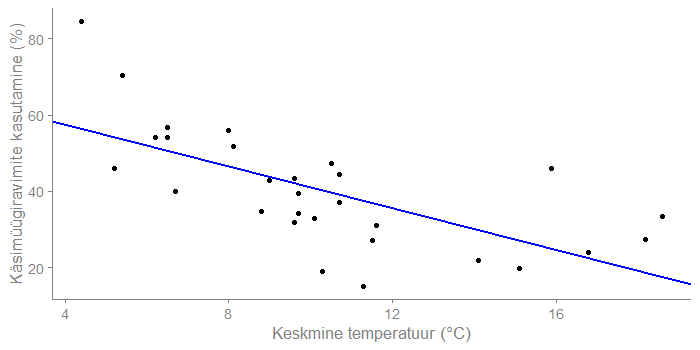
Antud mudeli vabaliige on 68,3 ja keskmise temperatuuri kordaja on -2,7. Mudel ütleb, et kui riigi keskmine temperatuur on 0°C, siis 68% inimestest võiksid olla kasutanud käsimüügiravimeid viimase 2 nädala jooksul. Iga kraadi tõus langetab seda 2,7 protsendipunkti võrra. Kui keskmine temperatuur on 10°C, siis hinnanguliselt 41% inimestest on kasutanud käsimüügiravimeid viimase 2 nädala jooksul.
Mitme seletava tunnusega mudel
Minu silmale tundub, et kui temperatuur on üle 13°C, siis hakkavad punktid jälle tõusma. Ma teen uue tunnuse juurde – keskmise temperatuuri ruudu. Ja proovin mitme seletava tunnusega regressioonimudelit, kuhu panen kõik ilma tunnused sisse.
mudel2 <- lm(kasutusprotsent ~ kesk_temp + temp_vahe + kesk_temp2 + sademete_hulk + sademete_paev + paikse_tunnid, andmed)
summary(mudel2)
> Call:
> lm(formula = kasutusprotsent ~ kesk_temp + temp_vahe + kesk_temp2 +
> sademete_hulk + sademete_paev + paikse_tunnid, data = andmed)
>
> Residuals:
> Min 1Q Median 3Q Max
> -19.320 -5.648 -0.318 4.505 17.253
>
> Coefficients:
> Estimate Std. Error t value Pr(>|t|)
> (Intercept) 9.968e+01 2.127e+01 4.687 0.000113 ***
> kesk_temp -1.177e+01 3.033e+00 -3.882 0.000804 ***
> temp_vahe -3.278e-01 6.026e-01 -0.544 0.592006
> kesk_temp2 3.468e-01 1.571e-01 2.208 0.037980 *
> sademete_hulk 8.404e-04 9.938e-03 0.085 0.933372
> sademete_paev 6.329e-02 6.757e-02 0.937 0.359108
> paikse_tunnid 9.614e-03 8.751e-03 1.099 0.283805
> ---
> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> Residual standard error: 9.805 on 22 degrees of freedom
> Multiple R-squared: 0.6895, Adjusted R-squared: 0.6048
> F-statistic: 8.142 on 6 and 22 DF, p-value: 0.0001034
Selles mudelis ei ole kõik tunnused olulised (kõigi ridade taga ei ole tärne), seega tuleb teha uus mudel. Selleks eemaldan tunnuse, mille olulisustõenäosus on kõige suurem – sademete hulk. Kontrollin uue mudeli tunnuste olulisust. Kui ikka ei ole kõik tunnused olulised, siis eemaldan uuesti kõige suurema olulisustõenäosusega tunnuse. Seda tsüklit kordan kuni kõik tunnused on olulised.
mudel3 <- lm(kasutusprotsent ~ kesk_temp + kesk_temp2, andmed)
summary(mudel3)
>
> Call: > lm(formula = kasutusprotsent ~ kesk_temp + kesk_temp2, data = andmed)
>
> Residuals:
> Min 1Q Median 3Q Max
> -18.6327 -4.1763 -0.7641 6.3402 19.4163
>
> Coefficients:
> Estimate Std. Error t value Pr(>|t|)
> (Intercept) 119.3936 13.8146 8.643 4.03e-09 ***
> kesk_temp -12.7865 2.5661 -4.983 3.52e-05 ***
> kesk_temp2 0.4375 0.1097 3.989 0.000482 ***
> ---
> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> Residual standard error: 9.514 on 26 degrees of freedom
> Multiple R-squared: 0.6545, Adjusted R-squared: 0.6279
> F-statistic: 24.63 on 2 and 26 DF, p-value: 9.992e-07
Selle mudeli R2 on 65% ja parandatud R2 on 63% ehk see mudel on parem kui mudel1. Ja selle mudeli kuju on
kasutusprotsent = 119,4 – 12,8 * keskmine temperatuur + 0,4 * keskmine temperatuur2.
Kui keskmine temperatuur on 10°C, siis hinnanguliselt kasutusprotsent on 119,4 -12,8*10 +0,4*100 = 31,4%.
Kokkuvõte
Lineaarne regressioon on mudel, mille kuju on
Y = α + β1X1 + β2X2 + β3X3 + … + ε,
kus Y on uuritav tunnus, X1, X2, X3 … on kirjeldav tunnus, α on vabaliige, β1, β2, β3 … on regressioonikordajad ja ε mudeli juhuslik viga. Kirjeldavaid tunnuseid võib olla üks või mitu.
Mudeldasin andmeid, millega proovisin seletada, kuidas ilm mõjutab käsimüügiravimite kasutamist Euroopa riikides. Uuritavaks tunnuseks on protsent inimestest, kes viimase kahe nädala jooksul on kasutanud käsimüügiravimeid (2014. aasta andmed).
Lihtsas lineaarses regressioonmudelis kasutasin seletavaks tunnuseks keskmist temperatuuri. Tulemuseks sain
kasutusprotsent = 68,3 – 2,7 * keskmine temperatuur
ehk iga kraadi tõusuga väheneb kasutusmäär 2.7 protsendipunkti võrra.
Mitme seletava tunnusega mudelis jäid seletavateks tunnusteks keskmine temperatuur ja keskmise temperatuuri ruut. Sademed ja päiksepaiste tundide arv ei olnud olulised. Tulemuseks sain
kasutusprotsent = 119,4 – 12,8 * keskmine temperatuur + 0,4 * keskmine temperatuur2.